Table of Contents
Algebra Formula
In below mentioned video, we elaborate basic reqirement of algebra formula and how to handle the issue.
नीचे दिए गए वीडियो में, हम बीजगणित सूत्र की बुनियादी आवश्यकता और इस मुद्दे को कैसे संभालना है, इसके बारे में विस्तार से बताया हैं।
What is Algebra?
Algebra is a specific branch of mathematics where letters and symbois are used to represent number.
बीजगणित गणित की एक विशिष्ट शाखा है जहाँ संख्याओं को दर्शाने के लिए अक्षरों और प्रतीकों का उपयोग किया जाता है।
Algebric Square Formulas of two components like a & b
1. (a + b)2 = a2 + b2 + 2ab
2. (a + b)2 = (a + b)(a + b)
3. (a – b)2 = a2 + b2 – 2ab
4. a2 – b2 = (a + b)(a – b)
5. (a + b)2 = (a – b)2+ 4ab
6. (a – b)2 = (a + b)2– 4ab
7. a2 + b2 = (a – b)2+ 2ab
8. a2 + b2 = (a + b)2– 2ab
Challenge to memorize Algebric Formulas
Without memorizing Algebric Formulas, it is absolutely impossible to score better marks in Algebra. To start Algebra, first and fonemost condition to memorize all important basic algebric formulas and students generally stuck up in memorizing process. Here we are providing you Flash card which help you to memorize the formula fast way without putting any pressure over you.
बीजगणितीय सूत्रों को याद किए बिना बीजगणित में बेहतर अंक प्राप्त करना बिल्कुल असंभव है। बीजगणित शुरू करने के लिए, सभी महत्वपूर्ण बुनियादी बीजगणितीय सूत्रों को याद करने के लिए पहली और सबसे महत्वपूर्ण शर्त और छात्र आमतौर पर याद रखने की प्रक्रिया में फंस जाते हैं। यहां हम आपको फ्लैश कार्ड प्रदान कर रहे हैं जो आपको बिना किसी दबाव के फॉर्मूला को तेजी से याद करने में भरपूर मदद करेगा।
Flash Card to memorize above 8 Formula
(a + b)2 = (a - b)?...
(a - b)2 + 4ab
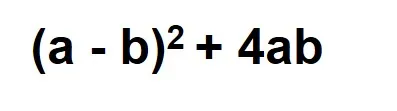
Question Explanation:
(a + b)2 =
Explanation (a - b)2 + 4ab
a2 + b2 - 2ab + 4ab
a2 + b2 + 2ab
=(a + b)2
(a - b)2 = (a + b)? + ..
(a + b)2 - 4ab
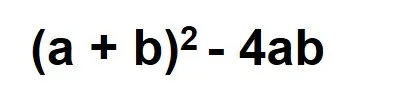
Question Explanation:
(a - b)2 =
Explanation (a + b)2 - 4ab
a2 + b2 + 2ab - 4ab
a2 + b2 - 2ab
=(a - b)2
Quiz on Above Algebric Formula
Algebric Formula of rest square & Cubic Formula
Here we have put 4 type of square formula with 3 symbols like x,y and z which are used in basic level math alnd cube formula which used frequently.
यहां हमने x, y और z जैसे 3 प्रतीकों के साथ 4 प्रकार के वर्ग सूत्र रखे हैं जो कि बुनियादी स्तर के गणित और घन सूत्र में उपयोग किए जाते हैं जो अक्सर उपयोग किए जाते हैं।
9.(x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2xz
10.(x + y – z)2= x2 + y2 + z2 + 2xy – 2yz – 2xz
11. (x – y + z)2 = x2 + y2 + z2 – 2xy – 2yz + 2xz
12. (x – y – z)2 = x2 + y2 + z2 – 2xy + 2yz – 2xz
13. (a + b)3 = a3 + b3 +3a2b + 3ab2
14. (a + b)3 = a3 + b3 + 3ab(a + b)
15.(a – b)3 = a3– b3–3a2b + 3ab2
16. (a – b)3 = a3 – b3 + 3ab(a – b)
Flash Card Practice
Which one is correct?
(x + y + z)2 =?
1) x2 + y2 + z2 + 2xy + 2yz + 2xz
2) x2 + y2 + z2 - 2xy - 2yz + 2xz
3) x2 + y2 + z2 - 2xy + 2yz - 2xz
4) x2 + y2 + z2 + 2xy - 2yz - 2xz
1
Question Explanation:
x2 + y2 + z2 + 2xy + 2yz + 2xz
Which one is correct?
(x + y - z)2 =?
1) x2 + y2 + z2 + 2xy + 2yz + 2xz
2) x2 + y2 + z2 - 2xy - 2yz + 2xz
3) x2 + y2 + z2 - 2xy + 2yz - 2xz
4) x2 + y2 + z2 + 2xy - 2yz - 2xz
4
Question Explanation:
x2 + y2 + z2 + 2xy - 2yz - 2xz
Which one is correct?
(x - y + z)2 =?
1) x2 + y2 + z2 + 2xy + 2yz + 2xz
2) x2 + y2 + z2 - 2xy - 2yz + 2xz
3) x2 + y2 + z2 - 2xy + 2yz - 2xz
4) x2 + y2 + z2 + 2xy - 2yz - 2xz
2
Question Explanation:
x2 + y2 + z2 - 2xy - 2yz + 2xz
Which one is correct?
(x - y - z)2 =?
1) x2 + y2 + z2 + 2xy + 2yz + 2xz
2) x2 + y2 + z2 - 2xy - 2yz + 2xz
3) x2 + y2 + z2 - 2xy + 2yz - 2xz
4) x2 + y2 + z2 + 2xy - 2yz - 2xz
3
Question Explanation:
x2 + y2 + z2 - 2xy + 2yz - 2xz
Which on is correct
(a + b)3 =?
1) a3 + b3 +3a2b + 3ab
2) a3 + b3 +3ab + 3ab2
3) a3 + b3 +3a2b + 3ab2
4) a3 + b3 +3a3b + 3ab3
3
Question Explanation:
a3 + b3 +3a2b + 3ab2
Which on is correct
(a - b)3 =?
1) a3 + b3 - 3a2b + 3ab2
2) a3 + b3 + 3ab(a - b)
3) a3 + b3 + 3ab(a + b)
4) a3 - b3 - 3a2b + 3ab2
4
Question Explanation:
a3 - b3 - 3a2b + 3ab2
Which on is correct
(a + b)3 =?
1) a3 + b3 +3a2b + 3ab
2) a3 + b3 + 3ab(a + b)
3) a3 + b3 +3ab + 3ab2
4) a3 + b3 + 3ab(a - b)
2
Question Explanation:
a3 + b3 + 3ab(a + b)




